令和6年度(2024)千葉県公立高校入試（国語・数学・英語）
鎌取・おゆみ野・誉田の学習塾 大桜塾です！
前回に引き続き令和6年度千葉県公立高校入試結果について分析していきます。
前回の記事はこちら
令和6年度(2024)千葉県公立高校入試平均点
鎌取・おゆみ野・誉田の学習塾 大桜塾です！ 本日令和6年度千葉県公立高校入試の平均点が発表になりました。 令和６年度平均点 入試年度 国語 数学 英語 理科 社会 ５科 …
大桜塾 
今回は国語・数学・英語の３教科の詳細を分析していこうと思います。
国語
平均点：５０．４点（前年４７．９点）
点数配分
●聞き取り・・・8点
●漢字、文法、言葉の問題等・・・18点
●説明的文章（説明文）・・・21点
●文学的文章（物語文）・・・23点
●古典・・・18点
●作文・・・12点
となっています。
点数配分に関しては前年とほとんど同じ構成でしたが、漢字の書き問題が１問減り４問となりました。
正答率分析
●正答率50％以上の問題・・・39点分（前年43点分）
●正答率20％以下の問題（10％以下の問題も含む）・・・28点分（前年26点分）
●正答率10％以下の問題・・・10点分（前年13点分）
となっていました。
正答率50％以上の問題が前年より減っているにもかかわらず、平均点が上がっているという結果となりました。
つまり出来た問題と出来なかった問題が生徒ごとに分散してしまい、正答率だけでは問題の難易度が計り知れない状況になってしまいました。
更に正答率10％以下の問題は長めの記述問題のみに集中していました。
そのため過去問演習の際には、正答率で問題を分類することなく、全ての問題を確認しておく必要があると考えられます。
まだ１年目なので、こうなった影響がマークシートによるものかどうかは、今後検証していく必要があります。
最後に、得点分布は以下のようになっていました。
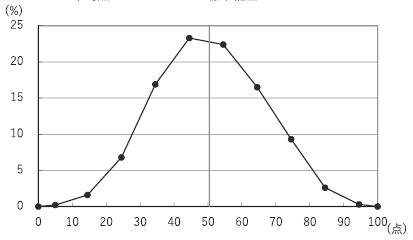
ピークが平均点より低いところにあり、正答率が下がっていた影響がみられると思います。
数学
平均点：５１．９点（前年４７．０点）
点数配分
●数と式（計算など）・・・21点
●図形・・・40点
●関数・・・27点
●データの活用・・・12点
となっています。
昨年大問の構成が変わり計算問題が減りましたが、本年は図形の問題数が多く、配分に偏りが出てしまいました。
正答率分析
●正答率50％以上の問題・・・55点分（前年50点分）
●正答率20％以下の問題（10％以下の問題も含む）・・・28点分（前年30点分）
●正答率10％以下の問題・・・14点分（前年24点分）
となっていました。
正答率50％以上の問題が増えたため、平均点も必然的に上がっています。
また正答率20％以下の問題は横ばいでしたが、10％以下の問題は10点分も減りました。上位校を目指す場合、数学の正答率の低い問題をどれだけ正解できるかで差がついていきます。そのため今回の問題では例年より数学では差がつきにくかったかもしれません。
そして、正答率が低い問題は関数と図形に集中していて、その点は例年通りの傾向になっていると言えます。
数学は学習する順番として、数と式➡データの活用、そのあと関数または図形としていった方が点数が安定してくかもしれません。
最後に、得点分布は以下のようになっていました。
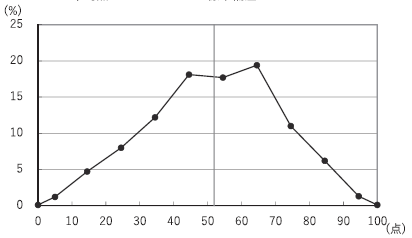
全体的な正答率が上がり、高難易度問題も減ったため、高めのところにピークがきています。
英語
平均点：５６．４点（前年４７．６点）
点数配分
●リスニング・・・27点
●文法、文構造・・・15点
●短文読解・・・21点
●長文読解・・・17点
●対話文・・・12点
●英作文・・・8点
となっています。
英語は何年もリスニングが33点分あったものが今年は27点分（2問減）となり、代わりに読解問題の配点が上がりました。
リスニングが減っていくと、試験時間がまた50分に戻っていくのではという不安も過ります。
正答率分析
●正答率50％以上の問題・・・66点分（前年36点分）
●正答率20％以下の問題（10％以下の問題も含む）・・・9点分（前年17点分）
●正答率10％以下の問題・・・5点分（前年10点分）
となっていました。
昨年に比べて圧倒的に正答率50％以上の問題が増えましたが、平均点は一昨年並みに戻っただけでした。つまり問題ごとの正解者がバラバラに分布してしまい、国語同様正答率だけでは計れなくなっています。
ただ国語とは逆に、正答率が高くても簡単な問題だとは考えない方がいいと考えられます。
また一番の違いは大問４のリスニング問題。
昨年までは単語を書かせる問題（単語のスペルを書く）が出題されていて、リスニング問題に組み込まれる前からの定番の問題でした。それが今回は単語問題が撤廃されていました。この影響は非常に大きく、単語のスペルを気にする練習をしなくてもよくなっていくかもしれません。
さらにマークシートによる影響かもしれませんが、全体として記述の問題も減っていました。
当然読解問題の一部や英作文のために単語を書く練習は必要不可欠ですが、目標点によってはカットしてもよいかもしれません。
ただこれでは英語力が落ちていってしまうのではないかと心配になります。
最後に、得点分布は以下のようになっていました。
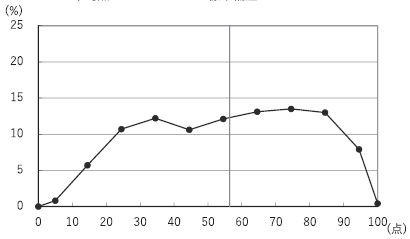
ピークのない独特な分布となっていますが得点が高い生徒も多く、そのために正答率が上昇したのだと考えられます。
次回は理科と社会について分析していきます。